College Tuition & Career Earnings

Robin Sifre
Last updated on Mar 17, 2020 4 min read Tidy Tuesday

I've recently started to participate in Tidy Tuesday, a weekly social data project in R.

This week, they shared an extremely rich dataset, on college tuition, diversity, and salary.

There is so much more I wanted to do with this data. But because I still have my PhD to finish, I limited myself. At the bottom of my code I commented out some interesting relationships between tuition and diversity that I didn't have time to pursue.

Here are some tweets from people who did pursue these questions:

The question(s)

  • We know that tuition has been rising - but is this true when we adjust for inflation? Is this driven by public or private schools?
  • What is the relationship between tuition and salary?

The rise of tuition

To answer this, I used the historical_tuition data, which has average college tuition data from 1985. I decided to look at dollar inflation adjusted tuition to aid in interpretability.

historical_tuition %>% 
  filter(tuition_type == 'All Constant') %>%# dollar inflation adjusted     
ggplot(data = ., aes(x = yr, y = tuition_cost, group_by(type), color = type) ) + 
  geom_point() +
  geom_line() + 
  theme_bw() + 
  theme(legend.background = NULL) +
  xlab('Year') +
  ylab('Tution ($ inflation adjusted)') + 
  scale_x_continuous(breaks = seq(1985, 2015, 5))
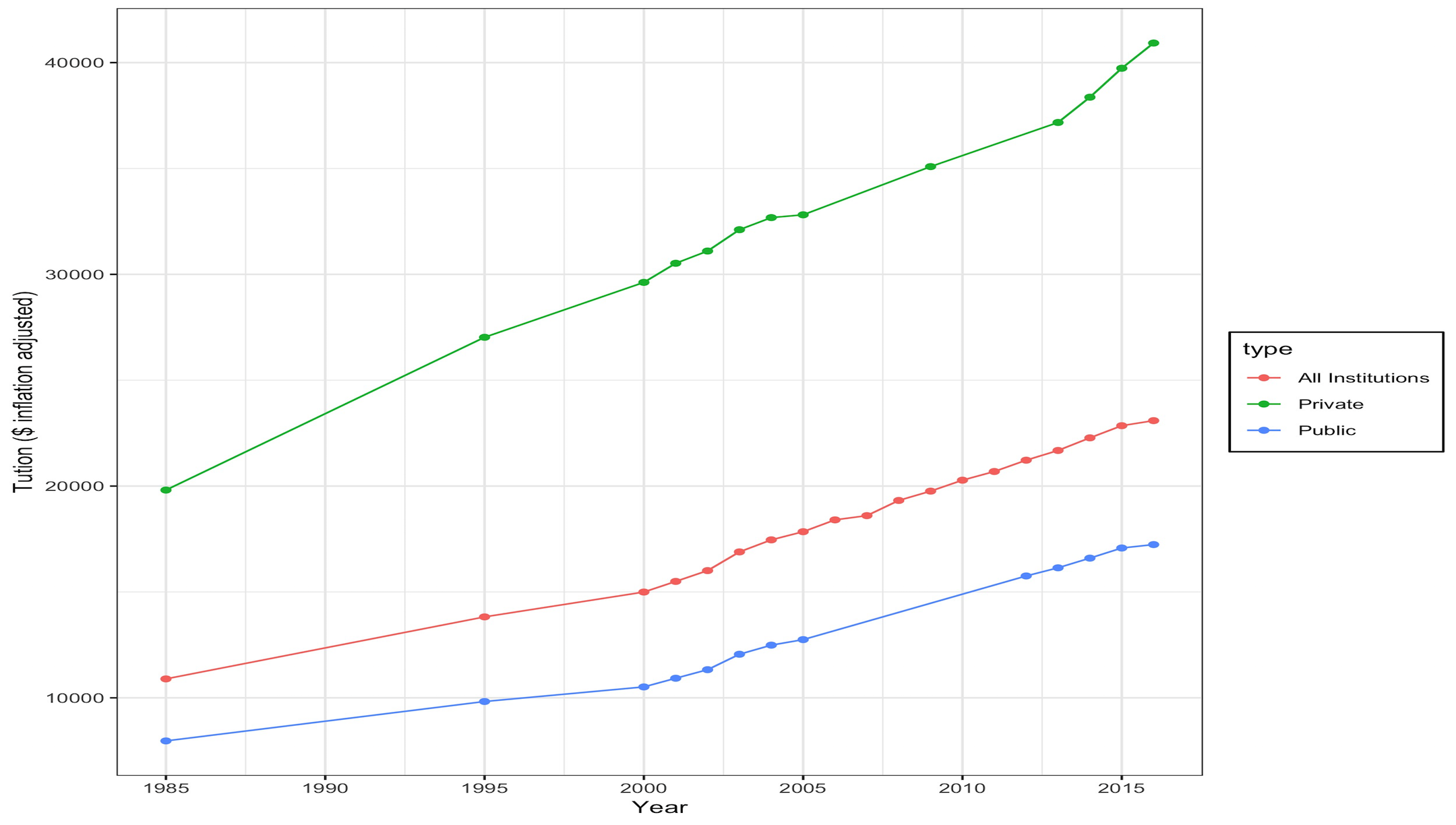As expected, tuition has been rising for both public and private universities (plotted in pink). Tuition for private institutions (green) appears to be increasing at a faster rate than Public institutions (blue).

  • Tuition is rising when we adjust for inflation.

  • It is rising in both Public and Private Institutions

Relationship between tuition and earnings

Next, I plotted the relationship between tuition and average early-career salary.

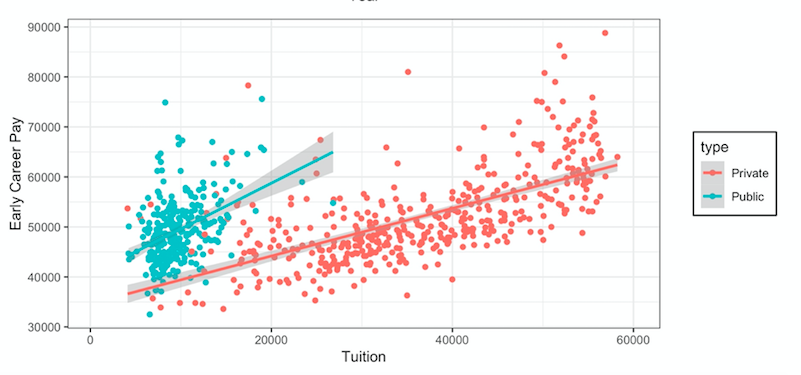From the image, there are a few noticeable trends:

  1. There seems to be a positive relationship between Tuition and Early-career salary.
  2. The relationship between Tuition and Early-career pay appears stronger for Public Institutions, rather than Private Institutions (in other words, the slope looks steeper). We're a bit limited here, though, since the range of tuition is lower for Public institutions.
  3. Early career pay looks higher, on average, for Public Institutions.

To test the statistical significance of these effects I used lme4 to build simple linear models in R.

lm.0 = lm(data = dat, early_career_pay ~ 1)
lm.1 = lm(data = dat, early_career_pay ~ 1 + in_state_tuition)
lm.2 = lm(data = dat, early_career_pay ~ 1 + in_state_tuition + public_dummy)
lm.3 = lm(data = dat, early_career_pay ~ 1 + in_state_tuition + public_dummy + public_dummy:in_state_tuition)
summary(lm.3)

Coefficients:
                               Estimate Std. Error t value Pr(>|t|)    
(Intercept)                   3.465e+04  9.699e+02  35.728  < 2e-16 ***
in_state_tuition              4.767e-01  2.524e-02  18.889  < 2e-16 ***
public_dummy                  5.792e+03  1.643e+03   3.525  0.00045 ***
in_state_tuition:public_dummy 4.384e-01  1.331e-01   3.293  0.00104 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

We can use these Estimates to better interpret this statistical model:

  • How much more are earnings for graduates when they attend schools with higher tuition?
    We know that for every $1 increase in tuition, earnings increase by $0.47 (all else equal). This means, a $5,000 increase in tuition is associated with $2,385 more in yearly earnings.

  • How much more are students at Public institutions earning? . The estimate for public_dummy tells us that on average, Students at Public institutions are earning $5,792 more. However, this is where “all else equal” becomes important. Not many Private schools are in the same tuition-range as Public schools. Students at the Private schools that cost more are out-earning the Public school students.

  • Seeing the forest through the trees.
    Our intercept estimate indicates that the average early-career salary is $34,650. With today's average yearly tuition hovering well-above $20k, it really makes you think about the bang for your buck when picking a school.

Feel free to post a comment here, or comment on my original tweet:

tidy tuesday R statistics ggplot data science
comments powered by Disqus

Related